As the rate-based congestion control framework proposed in this thesis shifts the majority of control into the routers within the network, the cost of this extra workload needs to be examined. In order for the framework to be practical, the benefits of the new control framework must outweigh the drawbacks of implementing it.
This appendix details the operations of RBCC within a router. To begin with, the data structures for RBCC are explored, indicating the memory requirements for the implementation of RBCC in a router. Following this, each specific operation of RBCC, its complexity and cost, will be described.
The overhead of RBCC on a router, in terms of both memory and CPU requirements, depends greatly upon the number of individual traffic flows passing through it at any given time.
[Apisdorf et al 96] describe a hardware-based OC3 network monitor for the NSF's very high speed Backbone Network Service. One of the functions of the network monitor is to measure the number of flows on an OC3 link. The definition of a traffic flow from the paper is given below.
We specifically do not restrict ourselves to the TCP connection definition, i.e., SYN/FIN-based, of a flow. Instead, we define a flow based on traffic satisfying specified temporal and spatial locality conditions, as observed at an internal point of the network. ... That is, a flow represents actual traffic activity from one or both of its transmission endpoints as perceived at a given network measurement point. A flow is active as long as observed packets that meet the flow specification arrive separated in time by less than a specified timeout value...
We explored a range of timeouts ..., and found that 64 seconds was a reasonable compromise between the size of the flow table and the amount of work setting up and tearing down flows between the same points...
We define flows as unidirectional, i.e., bidirectional traffic between A and B would show up as two separate flows: traffic from A to B, and traffic from B to A.
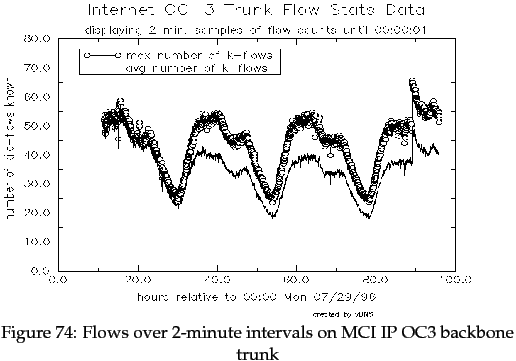
In [Apisdorf et al 96], one graph shows the number of flows ``on an OC3 trunk of MCI's IP backbone during the period between 29 July and 1 August 1996'', and is reproduced in Figure 74.
The graph shows that, during the trace period, the router sustained a peak of 67,000 traffic flows over a period of 2 minutes. Although this is a single data point, it indicates the order of magnitude for the number of flows across a core Internet router in late 1996.
The details of each traffic flow held by RBCC within a router are organised as per-interface `Allocation Bandwidth Tables'. The term `table' is a misnomer, as a linear list or array would most likely not be used. Instead, an implementation would choose a fast-search structure like a hash table or a B-tree. This would minimise search time of the table on receipt of a packet.
An individual flow's node within the table would include the following fields:
struct conv_type /* Table entry for a single flow */
{
/* Congestion fields */
double flow_id; /* Unique identifier for this flow */
int bottlenode; /* Node which is the bottleneck */
double rate; /* Rate allocated by a node */
double desired_rate; /* Rate desired by the source */
double lim_rate; /* Limiting rate on the flow */
/* Cached packet fields */
double cache_rate; /* Rate measured along the route */
double cache_desired_rate; /* Rate desired by the source */
int cache_bottlenode; /* node that last set the rate field */
/* Data structure fields */
struct conv_type *next; /* Pointer to next flow in the list */
struct conv_type *left; /* Pointer to left node in B-tree */
struct conv_type *right; /* Pointer to right node in B-tree */
};
The node belongs to two data structures:
On a machine where integers are 32-bits, pointers are 32-bits, and doubles are 32-bits, as described in Section 7.3, the node would occupy 44 bytes. On the router described in the previous section, at least 3 megabytes of memory would be required to hold all of the per-interface ABT tables.
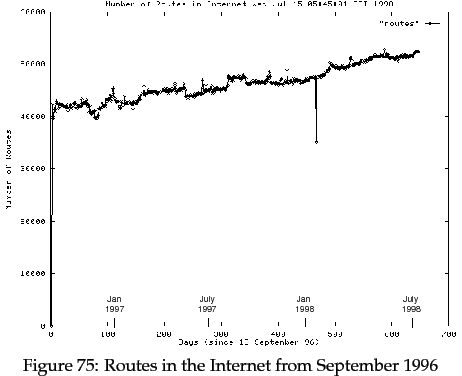
This compares well with the storage space required for the routing table in current Internet routers. The number of routes currently in the Internet is shown in Figure 75, taken from [Bates 98]. Current Internet routers typically store their routing table in a modified Patricia tree [Morrison 68]. Using a straightforward implementation of Patricia trees for a 32-bit processor, with 24 bytes for leaves and 24-bytes for internal nodes [Degermark et al 97], a routing table of 52,000 entries would occupy 2.5 megabytes of memory.
On current core Internet routers with 52,000 routing entries and 67,000 simultaneous traffic flows, the routing table and RBCC ABT storage costs are commensurate.
The CPU overhead of RBCC will be examined in this and following sections. Again, this overhead is related to the number of flows in the router's ABT tables. We will first consider the case of a packet arriving at a router which has an existing node with the Allocated Bandwidth Table; in other words, it is part of an already-recognised traffic flow. Packets for new flows will be addresses in the next section. Let us examine the RBCC operations that the router will perform.
RBCC is used after the router has has determined to which output interface the packet must be sent for retransmission, and before it is queued for transmission. The set of operations which RBCC must perform are:
The router must search the per-interface ABT B-tree for the given
flow_id in the packet. The order of complexity of
this operation will be O(log
N), with N the number of flows in
the B-tree (not the overall number of flows through the router).
This is the same complexity required to find the correct route, and
hence the correct output interface, for the
packet [Morrison 68].
The result of this operation is a pointer c, which points to the flow's entry in the per-interface ABT table.
This can be achieved with a bitwise comparison of the three congestion fields rate, desired_rate and bottlenode, between packet and cached values. The cost of this operation is O(1) and insignificant.
If the packet's congestion fields are found in the cache, then we may proceed to step 5.
This is described in detail in Section 6.2.2. Typically, 0.6% of packets reach this point, as is shown in Section 11.10.
if (pkt->desired_rate != c->cache_desired_rate) {
c->cache_desired_rate = pkt->desired_rate;
c->cache_bottlenode = pkt->bottlenode;
c->cache_rate = pkt->rate;
must perform ABT update;
}
if (we are not pkt->bottlenode and (pkt->rate != c->cache_rate)) {
c->cache_desired_rate = pkt->desired_rate;
c->cache_bottlenode = pkt->bottlenode;
c->cache_rate = pkt->rate;
must perform ABT update;
}
if (pkt->rate < c->cache_rate)
c->cache_desired_rate = pkt->desired_rate;
c->cache_bottlenode = pkt->bottlenode;
must perform ABT update;
}
Again, this operation is O(1) and insignificant. Common code inside the three test above can be aggregated to further reduce the CPU overhead. If we do not need to perform ABT updates, then we may proceed to step 5. As described in Section 11.4, reverse updates appear to be detrimental, and are therefore not considered here.
This is described in detail in Section 6.2.3. Typically, 0.3% of packets reach this point, as is shown in Section 11.10. The algorithm given in Section 6.2.3 is reproduced here with the comments removed.
bandwidth_left= bandwidth; flows_left= flowcount;
for (c= head_of_flow_list; c!=NULL; c= c->next) {
allocation = bandwidth_left / (1.0 * flows_left);
if (c->lim_rate > allocation) {
c->rate= allocation; c->bottlenode=node;
} else {
allocation= c->lim_rate; c->rate= allocation;
}
bandwidth_left-= allocation; flows_left--;
}
This operation is O(N), with N the number of flows in the per-interface B-tree (not the overall number of flows through the router). However, the amount of work inside the loop is small.
This is described in detail in Section 6.2.4. All packets must pass through this operation.
if ((pkt->rate > c->rate) || (we are the bottlenode)) {
pkt->rate = c->rate; pkt->bottlenode = c->bottlenode;
}
Again, this operation is O(1) and insignificant.
Operations 2 and 5 are O(1), and are done to all incoming packets.
Operation 3 is O(1) and is performed on 0.6% of all incoming packets.
Operation 1, a B-tree search, is O(logN), but each search step is short.
Operation 4, the core of the RBCC algorithm, is O(N), is the operation with
the highest cost.
If N, the number of nodes in each per-interface ABT, is smaller than the number of routes known by the router, then the cost of the RBCC algorithm (i.e operations 1 to 5) will be commensurate with, if not less than, the cost of determining the packet's route and output interface.
On receipt of a packet for a traffic flow which is not yet represented in any ABT within the router, a new flow node must be constructed and inserted in the appropriate table.
The construction pseudo-code is:
create a new node pointed to by conv;
conv->flow_id= pkt->flow_id;
conv->desired_rate = pkt->desired_rate;
conv->rate = pkt->rate;
/* Work out the correct bottle node */
if (pkt->rate == infinity) { conv->bottlenode = us; }
else { conv->bottlenode = pkt->bottlenode; }
/* Work out the limiting rate */
conv->lim_rate = pkt->desired_rate;
if ((pkt->bottlenode != us) && (pkt->rate < pkt->desired_rate))
conv->lim_rate = pkt->rate;
/* Cache the packet's fields */
c->cache_desired_rate = pkt->desired_rate;
c->cache_bottlenode = pkt->bottlenode;
c->cache_rate = pkt->rate;
The router must then perform two list insertions. The node must be inserted
into the B-tree on the basis of its flow_id value: this is an
O(logN) operation. The node must also be inserted into the singly-linked
list, ordered by the lim_rate value: this is an O(N) operation.
A flow node must be removed from the appropriate ABT when a traffic flow terminates normally (as described in Section 6.3.4), or when the loss of a flow is detected (as described in Section 6.3.5).
The removal of the node from the B-tree is an O(logN) operation.
The removal of the node from the singly-linked list is an an O(N) operation;
however, if a doubly-linked list was maintained instead, this operation
would become an O(1) operation.
Current routing tables within Internet routers tend not to change faster than once per second [Stanford 96]. If the output interface for a routing entry changes, then a router using RBCC must find the affected ABT entries, remove them from one per-interface ABT data structure, and insert them into a second per-interface ABT data structure. Although this is an O(N) operation, its frequency of occurrence is much lower then the operations considered previously.
The rate-based congestion control framework proposed in this thesis, and RBCC in particular, does place a higher load on routers within the network. Extra memory is required to hold the ABT data structures for RBCC, and for current core Internet routers, this is on the order of several megabytes of memory.
Of greater concern is the added processing burden that RBCC places on the
router. Most operations are O(1) and negligible, or O(logN) and similar
to the cost of finding the output interface for a received packet. Operation
4 in Section D.4 has the highest order of complexity,
O(N), and thus the highest cost. This cost is mitigated by the small number
of packets which undergo this operation (0.3%), the small amount of code
in Operation 4, and that N is the number of traffic flows exiting a single
output interface on the router.
A full implementation of RBCC in a real network router is required to accurately determine the full cost of the proposed rate-based congestion control framework. The estimations in this appendix, however, indicate that costs of RBCC are comparable to the current packet forwarding operations in Internet routers.