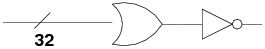Week 2 Tutorial - Building an ALU

1  Introduction

• This week, we are going to build an Arithmetic Logic Unit from scratch, using a handful of simple logic gates and other components.
• The ALU will take in two 32-bit values, and 2 control lines. Depending on the value of the control lines, the output will be the addition, subtraction, bitwise AND or bitwise OR of the inputs.
• Schematically, here is what we want to build:
  
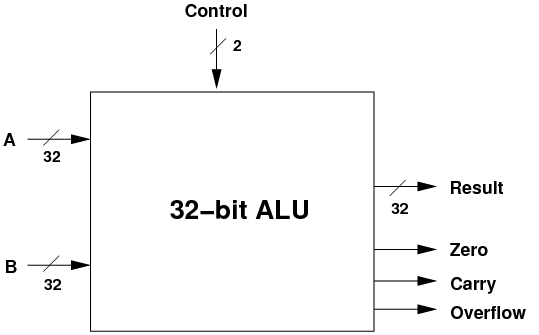
• Note! This is an interface for the ALU: what goes in, what comes out. It also shows the ALU as an abstraction: you can't see how it works, but you do know what it does.
• Also note that there are three status outputs as well as the main result: is the result zero, was there a carry, and did the operation result in an overflow?
• Note: just a reminder on the difference between a carry and an overflow:
  • Carry: was there a carry in the most-significant bit which we could not output in the given number of bits (32 bits, above).
  • Overflow: does the sign of the output differ from the inputs, indicating (for example) that a sum of two positive numbers has overflowed and is now a negative result!
• Some of the data and control lines are shown with a slash and a number like 32.
  
• This indicates that the line is actually 32 lines in parallel, e.g. the result is 32-bits wide. If you don't see a slash in the diagrams below, you can assume that the line is only 1-bit wide.

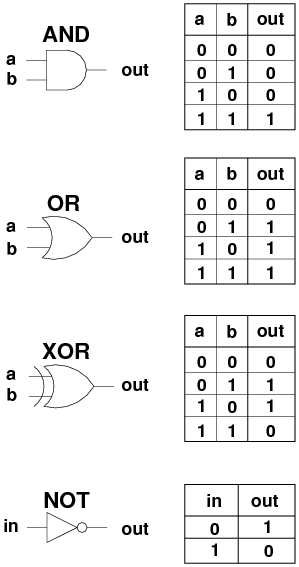
1.1  Basic Components

• We are going to use four logic gates: AND, OR, NOT and XOR. You should have seen these already in other subjects. Below are the icons for each, and their truth table.
  
• We are going to use another component, the multiplexor. The job of the multiplexor is to choose one of several inputs, based on a control line, and send the chosen input to the output.
  
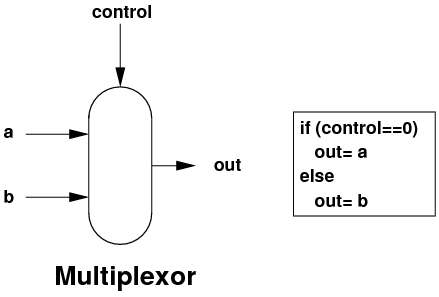
• This multiplexor above is a 1-bit wide 2-way multiplexor: 2 inputs, 1 bit wide each. If you add extra control lines, you can choose more inputs: 2 control lines is used in a 4-way multiplexor, 3 control lines in an 8-way multiplexor etc.
• And by using multiple multiplexors in parallel, you can make N-bit wide multiplexors.
• I'm not going to show you the internals of the multiplexor. You should, however, know that it can be easily built with the 4 logic gates above.

1.2  Bitwise AND

• Bitwise AND is very useful, for example to calculate an IP network's identity:
  • 131.245.7.18 AND 255.255.255.0 => 131.245.7.0
• Building the logic to do 32-bit AND on two inputs is easy: as each bit is independent, we just need 32 AND gates in parallel.
  
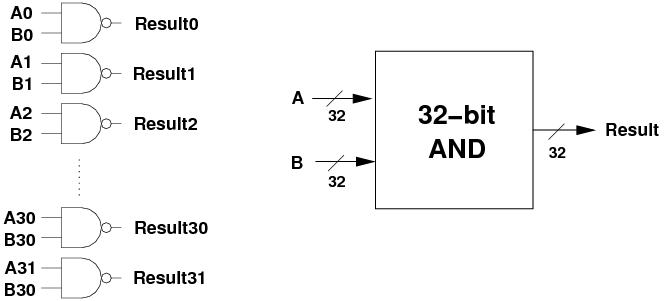
• Note the interface diagram on the right. Each time we build a larger component, we are going to hide it behind an interface.

1.3  Bitwise OR

• 32-bit bitwise OR is just as easy as bitwise AND, we just need 32 OR gates in parallel.
  

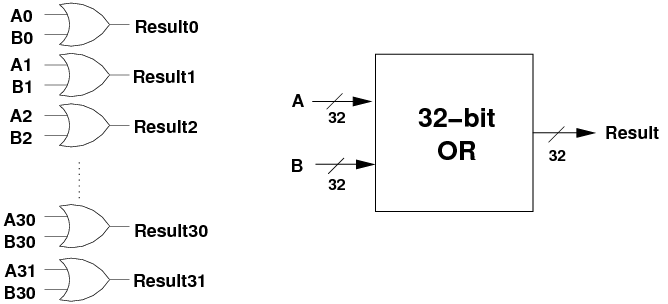
1.4  Addition

• Addition isn't going to be so easy.
• We saw previously that we have to add bits, and this may produce a carry. Columns further up need to accept a carry as input, along with two inputs, and produce the 1-bit output and another carry for the next column up.
• The component which will perform a 1-bit ADD, receiving a carry in and producing a 1-bit output and a carry out is called a full adder. Its interface looks like the following:
  
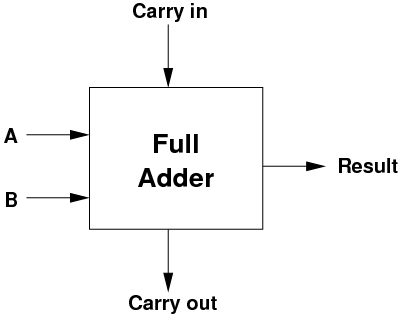
• Internally, here is what a full adder looks like, just 5 logic gates.
  
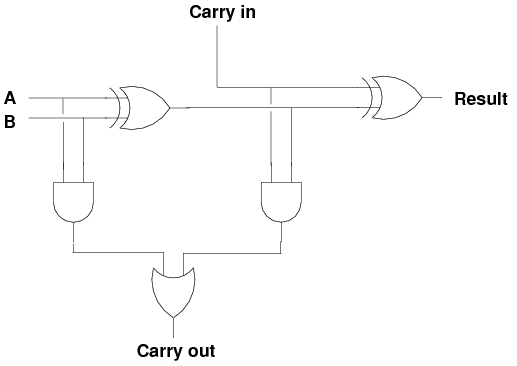
• The truth table for the full adder is:

  Cin	A	B	Result	Cout
  0	0	0	0	0
  0	0	1	1	0
  0	1	0	1	0
  0	1	1	0	1
  1	0	0	1	0
  1	0	1	0	1
  1	1	0	0	1
  1	1	1	1	1
• At some point sit down, try some inputs, and convince yourself that the logic works as advertised!
• To make a 32-bit full adder, we simply have to string 32 of these 1-bit full adders together.
• Except for the least-significant adder, each one is going to receive its carry from the one below and pass up its own carry to the one above.
• For the most significant bit, if the carry is a 1, then we ran out of bits to store the result.
  
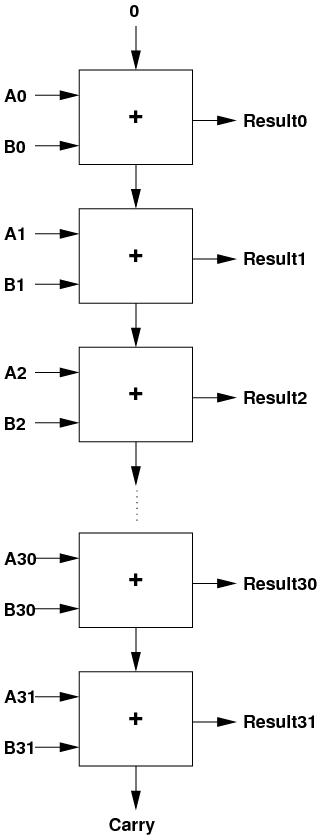
• When the final carry output is 1, this indicates that the result was too big to fit into 32 bits.
• I'm going to delay showing you the interface diagram for the 32-bit full adder, because we can modify it to also do subtraction.

1.5  Subtraction

• We could build a completely separate component, a 32-bit subtractor, once we work out how to build a 1-bit subtractor.
• Fortunately, we can simplify things a bit.
• According to the rules of maths: 3-2=3+(-2).
• If we could negate one of the inputs, we could use the existing 32-bit full adder.
• We have already seen two algorithms to negate a twos complement binary integer.
• One of them works as follows: invert every bit in the number, then add 1.
• Putting all of the above together, we can say:
  A - B = A + (-B) = A + ~B + 1
• Inverting every bit is easy: we can use a NOT gate for each bit in B.
• But now we need to do A + ~B + 1. How can we do this?
• We are going to use a very clever trick.
  • Set the initial carry-in to 1 instead of 0, thus adding an extra 1 to the sum.
  • And instead of using NOT gates, we will use XOR gates.
  
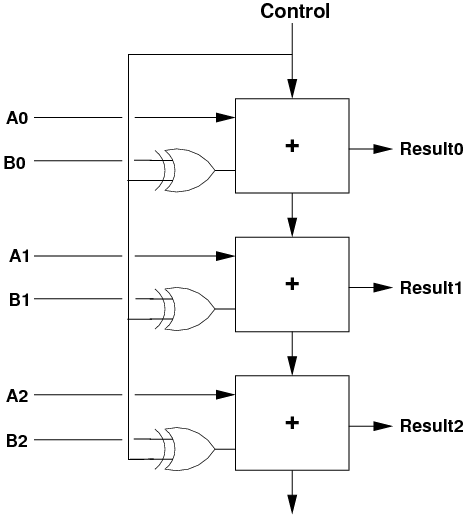
• If we are doing addition (Control=0), then one arm of the XOR gates is zero, and the B bits go into the adders unchanged, and the carry-in is zero.
• If we are doing subtraction (Control=1), then one arm of the XOR gates is one. This inverts all of the B bits before they get to the adders. As well, the carry-in is now 1, so we achieve the result of doing A - B = A + ~B + 1!
• Overall, we end up with this unit which can do addition and subtraction:
  
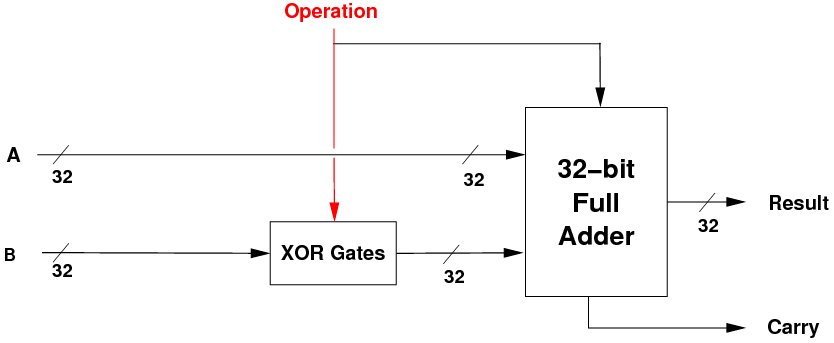
• If the operation bit is 0, we pass in B and perform A+B. If the operation bit is 1, we invert B and do A + ~B + 1.
• We can now distinguish between data lines (which pass data around) and control lines (which control the actions of the components).
• The data lines are also known as datapaths.
• The Operation line above is a control line, as it controls the action being performed. But note, it is also used as a 1-value for the carry-in, so it is also a piece of data!

1.6  Overflow Output

• We've seen that a carry occurs when the final addition or subtraction is too big to fit into 32 bits.
• A related mathematical output is overflow. This indicates that the sign of the maths result differs from the sign of the two inputs.
• Imagine we were using 4-bit numbers: you do 7 + 7 and get the result -2!
• Why? Because 7 (0111) + 7 (0111) = 1110, which in 4-bit twos-complement is -2.
• Overflow occurs when the size of the inputs is such that there is a carry which changes the most-significant sign bit.
• The ALU will always output both carry and overflow, but both only makes sense when the operation is add or subtract.
• When we are doing the logical operations (AND and OR), the values on the carry and overflow outputs have no meaning.
• As overflow is only maths related, this should be implemented in the ADD/SUBTRACT unit.
• The logic is follows: when adding, if the sign of the two inputs is the same, but the result sign is different, then we have an overflow.
• The boolean expression is [`a31]·[`b31]·result31+a31·b31·[`result31].
• We have to do this only for addition, so we take the b31 value after the XOR gate, i.e. just as it goes into the most-significant adder.
  

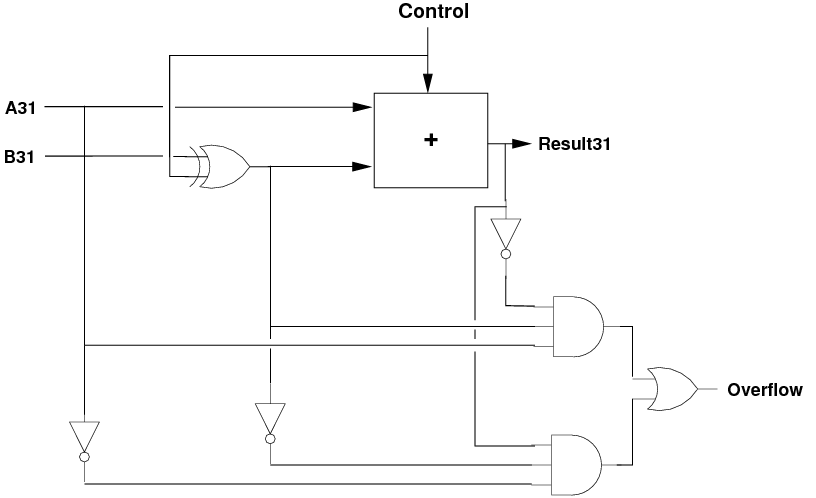
1.7  Negative Output

• When is the result negative? When its most-significant bit is 1.
• We can wire this bit directly out of the ALU, so that it indicates if the result is negative.

1.8  Zero Output

• One thing left to do is to provide the zero output: is the result zero?
• This is only true if all of the bits of the result are zero. We can do this for the logical and the maths units.
• To do this, we can use a 32-bit OR gate followed by a 1-bit NOT gate:
  
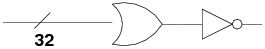
• The OR gate outputs a 0 only if all input bits are 0. If any input bit is a 1, the OR's output is a 1.
• The NOT gate simply inverts this, giving the result:
  • if any result bit is on, the output is 0, i.e. not zero.
  • if all result bits are off, the output is 1, i.e. zero.

1.9  Putting It All Together

• We are getting close to being able to build the full ALU.
• We now have three main units:
  • a 32-bit bitwise AND unit,
  • a 32-bit bitwise OR unit, and
  • a 32-bit ADD/SUBTRACT unit with a control line.
  • the logic to output carry, overflow, zero and negative.
• We can pass the inputs A and B to all three units, and perform all three operations in parallel:
  
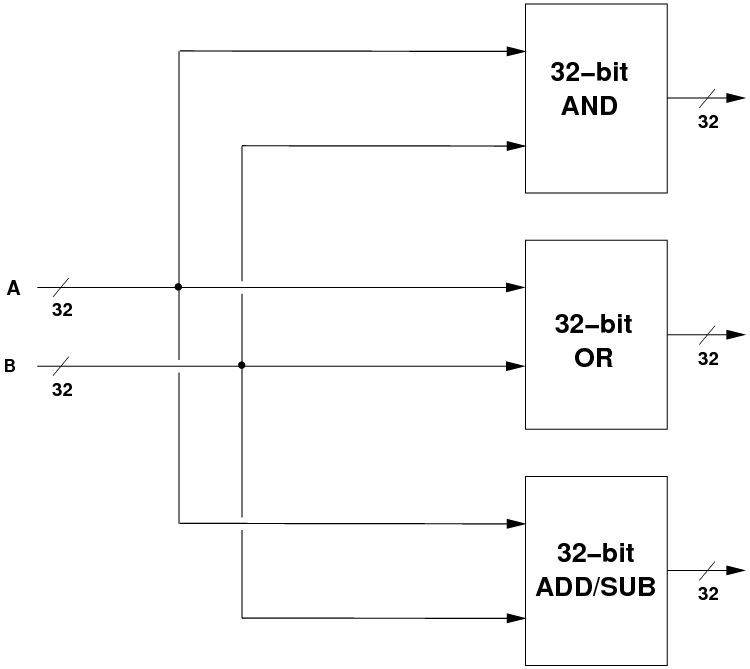
• But, we need to choose which of the three results we want, based on the two control lines coming into the ALU. We would like:

  c1	c0	Result
  0	0	A AND B
  0	1	A OR B
  1	0	A + B
  1	1	A - B
• How do we control which of the four operations actually becomes the result? With multiplexors again.
  
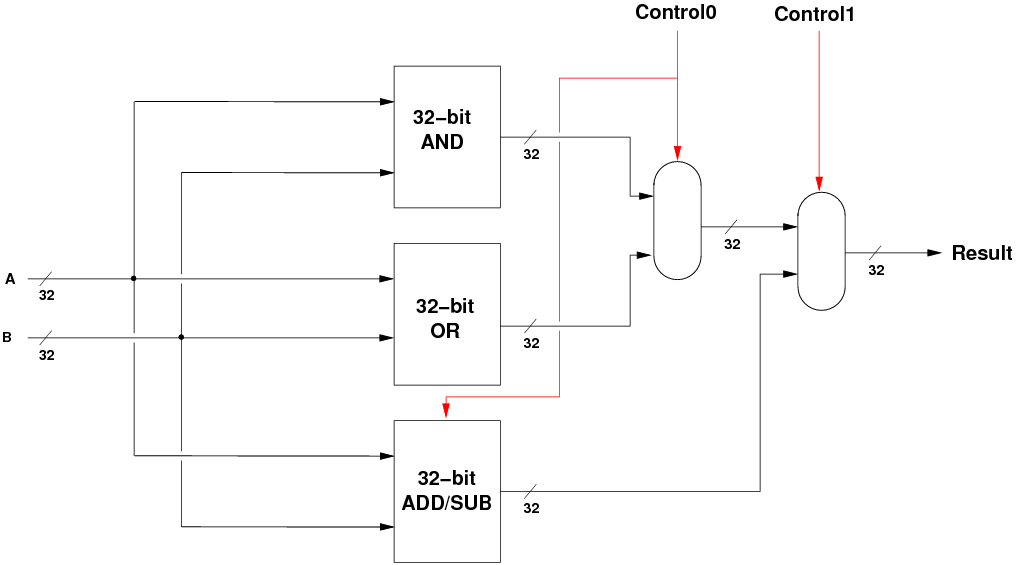
• When c₀=0, the ANDORresult is A AND B, and the ADDSUBresult is A + B.
• When c₀=1, the ANDORresult is A OR B, and the ADDSUBresult is A - B.
• Now we just have to choose between these two results, and that is done with the second multiplexor, which chooses either the bitwise logic result or the maths result.

1.10  Finally

• To finish off, we can draw the three components, the multiplexors and the zero logic, to reveal the final 32-bit ALU.
  
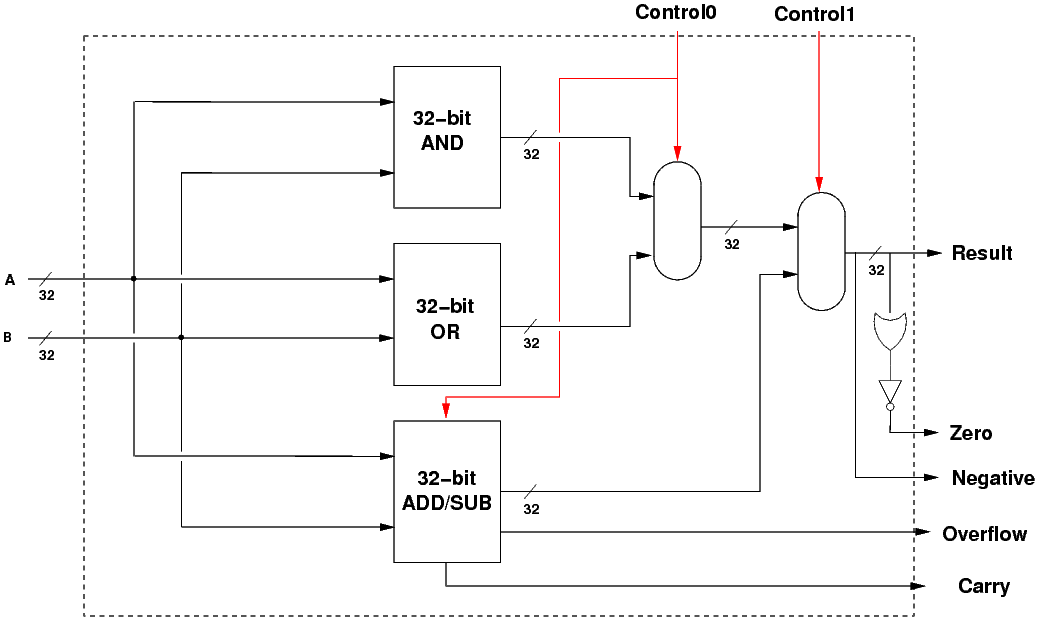
• The dotted line shows the interface to the ALU.

1.11  Implementing the ALU

• Here is the above ALU implemented in Logisim: ALUweek2.circ
• This is only an 8-bit version, but extending it to be a 32-bit CPU is simple but tedious.
• Download the file, run Logisim, and open the above circuit.
• Select the Hand icon in the top-left of the Logisim window, then click on the data inputs and the two control inputs to change their values.
• Try out some additions, a subtraction, some ANDs and ORs, and satisfy yourself that the ALU works as advertised.
• See if you can put in some input values which cause an oveflow.

1.12  Conclusion

• That's about all we can cover in terms of ALU design in this subject.
• Obviously, real ALUs perform many more operations, and use many performance optimisations.
• This is just a taste of ALU design, but you should now understand that:
  • an ALU is just a collection of logic components;
  • the logic components can be made from ordinary logic gates;
  • data can flow in parallel to multiple units;
  • everything operates in parallel: several units can produce output internally;
  • control logic, via multiplexors, chooses which output to use as the result.
• For more interested students, the ALU chapter in Patterson & Hennessy goes into much more detail and covers more operations such as multiplication and division.