Week 1 Tutorial - Data Representation
1 Introduction
- In this tutorial, we consider the issue of data representation: how
are different sorts of information represented inside a computer.
- We will look at integers, characters and floating point numbers.
- More complex data items, e.g. strings, colours, images, music etc.
can be represented by groups of the above.
- Before we start, there are several important things to realise:
- Everything has to be represented by a pattern of bits; in other words,
everything is a code. A specific value from the real world
is encoded as a specific pattern of bits in the computer. Some of
the encodings are algorithmic (e.g. integers, floats), whereas for
others the encoding is completely arbitrary (e.g. characters).
- For a fixed number of bits N, there are only 2N bit patterns.
If we choose fixed-size storage areas for data, this instantly constrains
the number of real-world data values we can represent.
- Above all, everything is just a bit pattern. While we tend to think
that computers perform maths, in reality many of the instructions
a computer performs are comparisons of bit patterns (equality, inequality,
ordering within a set etc.)
2 Integers
- Since the early 1970s, computers have settled on groups of 8-bit bytes
to represent data.
- Groups of bytes can be used to create storage cells of different sizes.
The most common data sizes today are:
- 8 bits, or 1 byte, which has 28=256 different bit patterns.
- 16 bits, or 2 bytes, which has 216=65,536 different bit patterns.
- 32 bits, or 4 bytes, which has 232=4,294,967,296 different bit
patterns.
- 64 bits, or 8 bytes, which has 264=18,446,744,073,709,551,616
different bit patterns.
- For integers, we let each bit in a bit pattern represent a different
power of two. A specific bit pattern represents the number which is
the sum of the powers of two of the bits which are ones.
- Traditionally, the right-most bits in a pattern store the lowest powers
of two: they are the least-significant bits. For example:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
2.1 Hexadecimal Bit Patterns
- Long bit patterns are unwieldy for humans, so an alternate way to
write bit patterns is to use hexadecimal.
- Groups of 4 bits are represented by a single character. As 4 bits
has 24 patterns, we need 16 different characters.
- The normal hexadecimal character set is 0 ... 9, followed by A ...
F. We use this table to match each bit pattern to a character:
| 0000 = 0 | 1000 = 8 |
| 0001 = 1 | 1001 = 9 |
| 0010 = 2 | 1010 = A |
| 0011 = 3 | 1011 = B |
| 0100 = 4 | 1100 = C |
| 0101 = 5 | 1101 = D |
| 0110 = 6 | 1110 = E |
| 0111 = 7 | 1111 = F |
- 8-bit patterns are 2 hex digits, 16-bit patterns are 4 hex digits,
32-bit patterns are 8 hex digits.
- We will use hex a lot in this subject, and we will follow the C and
Java convention of writing hex number preceded by "0x", e.g.
0xFF, 0x304D, 0x00010E4A.
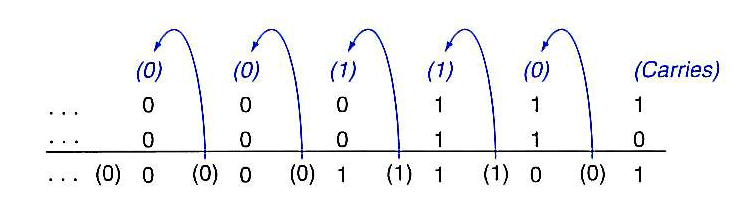
2.2 Rules of Addition and Subtraction
- Binary addition and subtraction work just like they do in decimal,
but they are in fact easier as there are only two symbols, not ten.
- For binary addition, instead of carrying a 1 when the result exceeds
nine, we carry a 1 when the result exceeds 1. The carry represents
the power of two in the next-biggest column.
- And just like subtraction, we need to borrow a 1 from the next column
if a column subtraction would give a negative result. Again, the borrow
represents the power of two in the next-biggest column.
- Quick exercise: add decimal 839406 + 153728 together on paper. Watch
the carries!
- Quick exercise: subtract decimal 58493 - 26548 on paper. Watch the
borrows!
- Binary addition rules:
| 0+0=0 |
| 0+1=1 |
| 1+0=1 |
| 1+1=0 carry 1 |
- Binary subtraction rules:
| 0-0=0 |
| 1-0=1 |
| 1-1=0 |
| 0-1=1 borrow 1 |
 (from Patterson & Hennessy)
(from Patterson & Hennessy)
2.3 Signed Integers
- The encoding of integers we are using (each bit represents a power
of two) has no way of representing negative numbers.
- For any bit pattern size, we would like to be able to choose if the
pattern represents an unsigned integer or a signed integer (one that
could be positive or negative).
- Moreover, for the signed integers, it makes sense to have half the
bit patterns represent positive numbers, and the other half negative
numbers.
- Note: the bit pattern doesn't know if it is representing a signed
or unsigned integer.
- 1011 0110 0001 1000 could be a signed or an unsigned 16-bit integer.
- As programers, we need to remember which data storage is holding what
type of value. In C:
short a; # 16-bit signed storage
unsigned short b # 16-bit unsigned storage;
- The next question is: how do we represent signed numbers? The only
real difference is knowing if the number is a +ve or a -ve one.
- Why not choose one of the bits in the pattern (usually the left-most
bit) and treat it as the sign bit: 0 represents +ve, and
1 represents -ve.
- This is known as signed-magnitude notation. While it works,
it has two big problems. We will use 8-bit examples below.
- Problem 1: there are now two values for zero: 00000000 and
10000000.
- Why is this a problem? Let's have short x and short
y. Let x have the 00000000 pattern, y have the
10000000 pattern. Both are zero.
- If we do if (x == y), the CPU will compare the bit patterns,
see they are different, and conclude that x != y, whereas
they are both zero.
- Problem 2: signed-magnitude notation does not follow the
binary rules of addition nor subtraction.
- As an example, let's do +5 + (-3). The answer should be +2.
00000101 +5
+ 10000011 -3, note the sign bit on the left
----------
10001000 i.e. -8
- What happens instead: the unsigned sections get added together, then
the sign bits get added together!
- So, signed-magnitude notation doesn't really work. We need another
representation for signed integers.
2.4 Twos-Complement Notation
- In twos-complement notation, the left-most bit still represents
the sign: 0 represents +ve, and 1 represents -ve.
- For positive bit patterns, the columns still represent powers of two
like they did before.
- But not for negative numbers!!
- Instead, a negative number is represented by that pattern when, when
added to the positive value, gives us zero.
- For example, -3 is represented in 8-bit twos-complement notation
as 11111101. Let's add this to +3:
11111101
+ 00000011
----------
00000000
- The advantages of twos-complement representation of signed integers
are that there is only one bit pattern for zero, and negative bit
patterns still work for both addition and subtraction.
- I recommend that you decode positive binary numbers by adding the
columns together,
- but DON'T try to read or decode a negative number, as it
doesn't work.
- Instead, visualise negative numbers like a car trip meter (odometer):
negative numbers are a certain distance "away" from zero. For
example, using 4-bit groups:
| -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
- Why is this analogous to the odometer? The number below 0000 on the
odometer is 9999, because 9999 + 1 kilometre will bring you back to
0000.
- Other things to note from the above table:
- Half the bit patterns are negative, and half are positive. We treat
0 as one of the positive integers, so we get these ranges:
- 8 bits, or 1 byte: -128 ... +127
- 16 bits, or 2 bytes: -32,768 ... +32,767
- 32 bits, or 4 bytes: -2,147,483,648 ... +2,147,483,647
- 64 bits, or 8 bytes: -9,223,372,036,854,775,808 ... +9,223,372,036,854,775,807
- Odd numbers always have their least-significant bit set, and even
ones don't.
- While not strictly a data representation issue, we should also think
about:
- Carry: if we add two 32-bit numbers, say, and the result
is so large that it won't fit back into 32 bits because of the carry
bit which falls off the left?
- Similarly, if we add or subtract negative numbers, and the result
is again below the most negative number, so it won't fit back into
32 bits.
- Overflow: if we add two positive, signed, 32 bit numbers,
say, and the result ends up with the most-significant bit set. This
indicates that the number is negative, which it isn't. This problem
when the sign bit of the output differs from the sign bits of the
input is known as overflow.
- Similarly, for subtraction, we get underflow.
- We will revisit the topic of carry, overflow and underflow later on.
2.5 Endianness
- When we choose to use 16-, 32- or 64-bit patterns, we need to store
the patterns in consecutive bytes in memory.
- For example, the 32-bit hex pattern 0x1203F5C4 would need to be stored
as 0x12, 0x03, 0xF5 and 0xC4 byte values.
- We have a choice: in what order should the byte values be stored?
- From a human's perspective, it makes sense to put the pattern into
memory in the same way that we write it down: big-end first, i.e.
| Byte Address | 0 | 1 | 2 | 3 |
| Value | 12 | 03 | F5 | C4 |
- This is known as big-endian storage of multi-byte data.
- However, this is completely arbitrary. There is another way to store
the byte values.
- Instead, we could store the byte values little-end first, or little-endian
storage, i.e.
| Byte Address | 0 | 1 | 2 | 3 |
| Value | C4 | F5 | 03 | 12 |
- This might seem weird-looking, but there is a reason for it. Consider
the small number 0x00000005, which is 5 decimal. Let's store it as
a 32-bit value at address 0 in memory, little-endian order:
| Byte Address | 0 | 1 | 2 | 3 |
| Value | 05 | 00 | 00 | 00 |
- Now, what 8-bit integer is stored at address 0: well, 0x05 of course,
or 5 decimal.
- And, what 16-bit little-endian integer is stored at address 0: well,
0x0005, which is again 5 decimal.
- But if, instead, we had stored the 32-bit value in big-endian order:
| Byte Address | 0 | 1 | 2 | 3 |
| Value | 00 | 00 | 00 | 05 |
the 8-bit and 16-bit equivalents are no longer at address 0: they
are at addresses 3 and 2, respectively.
- The decision to use big- or little-endian has been a running source of arguments
since the 1970s.
- Most CPUs are either little-endian or big-endian, but not both:
- Intel IA-32 chips are little-endian.
- Motorola 680x0 chips are big-endian.
- However, the MIPS CPU can be told to boot into either mode. We will
be using little-endian MIPS.
- It is worth noting that the default encoding of multibyte binary integers
on the Internet is big-endian format.
3 Characters and Strings
- There is no algorithmic way to convert characters into bit patterns.
- Therefore, we need an arbitrary mapping of characters to bit patterns,
known as a code.
- The most common character code is ASCII. It uses 7-bit patterns, normally
stored in 8-bit bytes with a leading 0 bit, to represent 128 characters.
- some characters are printable, including the space character.
- some characters are non-printable, but have been used to control character
transmission, e.g. to physical devices like teleprinters.
- The first 32 characters (0 to 31) are the control characters, ctrl-@,
ctrl-A ... ctrl-Z, ctrl-[, ctrl-\, ctrl-], ctrl-,
ctrl-_
- Then punctuation characters 32 to 47: space ! " # $ % & '
( ) * + , - . /
- Then the digits at positions 48 to 57: 0 ... 9
- Then more punctuation characters 58 to 64: : ; < = > ? @
- Uppercase characters are positions 65 to 90: A ... Z
- More punctuation characters 91 to 96: [ \ ]
_ `
- Lowercase characters are positions 97 to 122: a ... z
- Finally, more punctuation characters 123 to 127: { - }
DEL
- That last character, DEL, is really a control character, used to delete
the previous character.
- As ASCII characters are stored in 8-bit bytes, they can also be represented
as 2-digit hex numbers. Here are the printable ones:
 so 0x4B is 'K', 0x66 is 'f', 0x52 is 'R', 0x7A is 'z'
etc.
so 0x4B is 'K', 0x66 is 'f', 0x52 is 'R', 0x7A is 'z'
etc.
- Character strings can be stored as consecutive characters in memory.
Question: how do we know where the string stops?
- The Java solution is to keep an integer nearby which holds the string's
length, e.g "hello" might be stored as the 16-bit integer 5
followed by 'h' 'e' 'l' 'l' 'o'.
- The C solution is to store consecutive characters and then append
one final byte value, 0x00, as the end-of-string marker. This byte
value is also known as NUL.
- The advantage of the Java approach: the string's length is always
precomputed.
- The advantages of the C approach:
- at least one byte saving!
- no possibility of an inconsistency between the string and its length,
e.g. 5 and "consequences".
- cool things like replacing a character in the middle of the string
with a NUL to make it into 2 strings.
- We will be using NUL-terminated strings in the MIPS assembler, and
with C, during the subject.
- Internally, most CPUs don't know about characters: they are just bit
patterns, which means:
- we can do comparisons: ==, !=, and also > (comes after) and < (comes
before).
- this is why if (ch >= 'A' && ch <= 'Z') works in
Java.
- we can treat characters as 1-byte integers: 'A' + 3 gives us 'D' etc.
3.1 Unicode
- ASCII is only useful for English speakers: it does not have the range
of bit patterns to encode all the characters used in the many human
languages used around the world.
- Now, most systems are migrating up to encode characters using Unicode.
- Unicode defines a codespace of 1,114,112 code points (i.e.
bit patterns) in the range 0x00 to 0x10FFFF. Each code point represents
a specific character.
- The range of code points is broken up into a number of planes,
or sub-ranges:
- 0x0000 to 0xFFFF is the Basic Multilingual Plane, which holds most
of the useful human characters.
- 0x10000 to 0x1FFFF is the Supplementary Multilingual Plane, which
is mostly used for historic languages, but is also used for musical
and mathematical symbols.
- 0x20000 to 0x2FFFF is the Supplementary Ideographic Plane, which holds
Unified Han (CJK) Ideographs that were mostly not included in earlier
character encoding standards.
- The code points 0x30000 upwards are either reserved for private use,
or unassigned.
- Although technically Unicode characters require 21-bits, many programming
languages (e.g. Java) and libraries support the Basic Multilingual
Plane and use the 16-bit values 0x0000 to 0xFFFF to hold Unicode characters.
- Again, the CPU is oblivious to the Unicode-ness of a pattern, but
we can still do 16-bit comparisons etc.
- For efficient transmission and storage of Unicode data, it is usually
sent/stored using UTF-8 or UTF-16 format.
- We will not be covering Unicode in any greater depth in this subject,
as it's mainly an issue for libraries and programming languages.
4 Representation of Floating-Point Numbers
- We now come to the most complex of all the data representation topics,
that of floating point numbers.
- To make it a bit easier, I'm going to do most of the discussion in
decimal, and at the end switch over to binary.
- Before we start, it's important to remember that:
- There are an infinite set of floating-point numbers, even between
0.0 and 1.0.
- Given any fixed number of bits, e.g. 32 bits, there is only a finite
set of patterns.
- Implication: not all floating-point numbers can be represented accurately
with a fixed-size bit pattern.
4.1 Design Goals
- We saw with signed-magnitude that the most obvious solution comes
with drawbacks.
- So, this time we are going to start with some goals that we want to
achieve with the representation of floating-point numbers.
- We are able to represent both positive and negative numbers.
- We are able to represent very large numbers (large, positive exponents)
and very small numbers (large, negative exponents).
- There is a unique bit pattern for every floating-point number that
we can represent: no number can be represented by two or more bit
patterns.
- The pattern for 0.0 corresponds to the integer version of 0, i.e.
all zero bits.
- It would be nice to be able to represent certain mathematical results
for certain operations, e.g. 1/0 is infinity, and 0/0 is an undefined
result.
4.2 Scientific Notation
- To achieve goals 1 and 2, we really need to use scientific notation
as we do on calculators.
- Each decimal floating-point number has a mantissa (the part
of a floating-point number that contains its significant digits),
a sign (is the number positive or negative?), an exponent
(the power of 10 to which the mantissa is raised) and the exponent's
sign (a small power of 10 or a large power of 10).
- As an example, here is a decimal floating-point in scientific notation:
+7.83747*10+6
- The mantissa is 7.83747, the sign is +ve, the exponent is 6, and the
exponent's sign is +.
- In layman's terms, the value is around 7.8 million.
- We now have met goals 1 and 2, but unfortunately not goal 3. Why not?
- Because we can write +7.83747*10+6, +78.3747*10+5, +0.783747*10+7
and +0.0783747*10+8, and each one of them is the same number.
We can shift the decimal point around, and compensate by changing
the exponent.
- To solve this problem, we enforce a rule: there must always be exactly
one digit before the decimal point, and it can't be a zero!
- Now let's set a storage size goal: can we write the number +7.83747*10+6
as 10 characters only?
- Sure, we can write
- This gives us 6 digits of accuracy in the mantissa, two sign characters,
and an exponent range of 10-99 to 10+99.
- Note that we don't have to encode the base, 10, which we raise using
the exponent. That's implied.
- Similarly, the rule says that there is a decimal point after the first
digit, so there is no need to store that either.
- Question: what number is
written in normal scientific notation and in normal decimal notation?
- Moving on to goal 4. Let's assume in binary that + signs are represented
by zeroes, and - signs by ones. Then the number 0.0 is
which is all zeros.
4.3 The IEEE 754 Floating-point Standard
- Floating-point has been beset with data representation issues from
the beginning of computing, along with many other issues such as accuracy,
rounding errors, overflows and underflows, and dealing with infinity
and results which are not numbers.
- In the 1980s, after several years of wrangling, IEEE defined the 754
standard for representation of floating-point numbers as binary patterns.
We are only going to touch on the most important aspects of the data
representation. We are also going to look at single-precision floats
stored in 32 bits.
- The IEEE 754 format for floating-point numbers looks like the following:
 (from Patterson & Hennessy)
(from Patterson & Hennessy)
- The mantissa (or fraction) is 23 bits long, which is about 8 decimal
places long.
- Just as with our decimal representation which had a non-zero leading
digit before the decimal place, so too does IEE 754.
- But the only non-zero digit in binary is a 1, so if it never changes,
then there is no need to store it: its existence is implied.
- Therefore, the real mantissa always starts with an implied "1.",
followed by the mantissa stored in bits 22 down to 0.
- Each bit in the mantissa is a power of two which comes after the "decimal"
place, i.e. the "decimal" place is implicitly to the left of
bit 22.
- Bit 22 represents 0.12 or 1/2. Bit 21 represents 0.012
or 1/4. Bit 20 represents 1/8 etc.
- Therefore, if bits 22 downward held the pattern 110000 ... 0000, this
would represent 1.110002, or 1 + 0.5 + 0.25, or 1.75.
- Now we turn our attention to the exponent. This is the power of two
which the mantissa is multiplied by.
- Note that the exponent doesn't seem to have a sign bit.
- In fact, the exponent field holds an 8-bit unsigned value from which
we subtract 127 to get the actual power of two.
- This is called biased notation, where the exponent has a
bias (in this case, 127) subtracted to get the real power of two.
- Finally, the most-significant bit, bit 31, is the sign of the number:
0 is positive, -1 is negative.
4.4 Some Examples of IEEE 754 Numbers
- It's time for some numbers: let's see if we can convert them into
decimal. We start with:
0 01111111 11000000000000 ...
- The sign bit is 0, so it is positive.
- The exponent is 011111112, i.e. the number just before 128,
i.e. 127. So the real exponent is 127-127=0.
- The mantissa is 11000...., to which we prepend the implied "1.",
giving 1.110002, or 1 + 0.5 + 0.25, or 1.75.
- Putting this all together, we have +1.75*20. Now 20=1,
so the result is 1.75*1=1.75.
- Let's try another one:
1 00001111 0011100000 ...
- Taking it in stages:
- sign bit is 1: negative
- exponent is 15, so the real exponent is 15-127=-112 , i.e. we will
do 2-112.
- mantissa is 1.00111000 ...., i.e. 1 + 1/8 + 1/16 + 1/32 = 1.21875.
- Altogether, the number is -1.21875*2-112, or -2.3472271*10-34.
4.5 Other Features
- What floating-point value is the all-zeroes pattern 0 00000000 00000
... ?
- Technically, this is +1.0*2-127, i.e. around 7*10-46,
but in fact IEEE 754 defines this as exactly +0.0.
- Interestingly, the standard allows for 1 00000000 0000 ..., or -0.0!
This violates our rule 3: no number represented by multiple patterns.
- The highest exponent pattern, 11111111, is reserved to represent special
numbers.
- With this exponent and the mantissa set to all zeroes, this pattern
represents infinity, i.e. the result of N/0.
- With this exponent and any one bit set in the mantissa, this
pattern represents "not a number", written as NaN,
which is the result of doing 0/0 and some other interesting floating-point
operations.
4.6 Sorting Floating Point Numbers
- Question: how are floating-point numbers sorted?
- The 3 fields in the IEEE 754 format are placed so that we can do signed
integer comparison to sort floating-point numbers.
- The signed-bit is the most-significant bit, so that it appears as
a normal integer sign bit.
- The smallest exponent, 00000000, represents the smallest power of
two. The biggest usable exponent, 11111110, represents the biggest
power of two.
- So, a comparison of the exponent fields works just like the most-significant
bits of a normal integer.
- And, following that are the mantissa bits. Again, these work just
like the least-significant bits of a normal integer.
4.7 More Information
- For more details about floating-point representation, the relevant
chapter in Patterson & Hennessy is excellent.
- In the MARS simulator, there is a tool which you can use to convert
between decimal and IEEE 754 floating-point representation: it works
even without an assembly program:
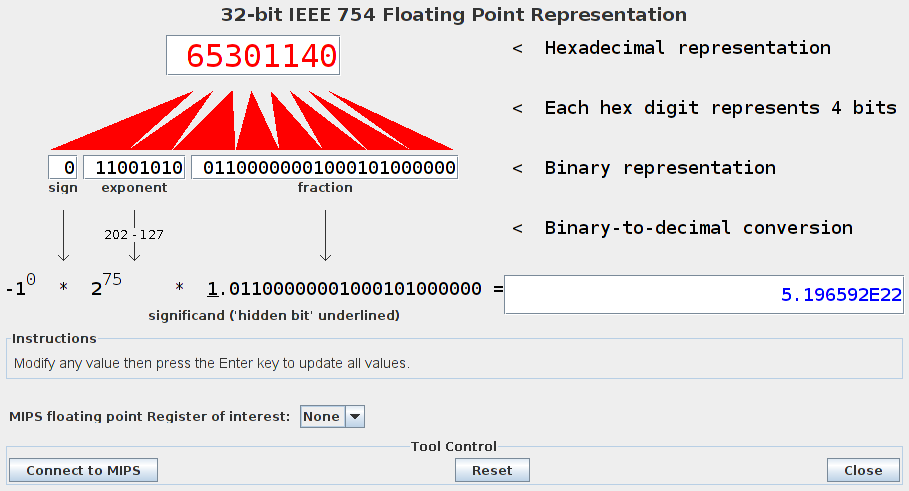
File translated from
TEX
by
TTH,
version 3.85.
On 19 Jan 2012, 06:12.




