System Architecture

(INFT12-212 and 72-212)

Lab Notes for Week 4: Calling Functions, The Stack, Complex Data Structures

1 Introduction

This week we are looking at the mechanism used on the MIPS CPU to call functions, so that programs can be modularised as we can in high-level languages like C and Java. To understand how we do this, we also need to understand the stack frame which MIPS uses. Later on, we will look at recursion in assembly.

2 Instructions for Calling and Returning

MIPS provides two instructions for calling functions and returning from functions:

jal label: Jump to the instruction at the named label, storing the address of the instruction following the jal in the $ra (return address) register.
jr $ra: Jump back to the instruction at the address stored in the $ra (return address) register.

These are the only instructions we need to do function calls; however, things are not as simple as they seem.

2.1 Task 1

Download the program wk4jal_jr_instructions.asm and load it into MARS. This program starts in the main() program, which prints out one string. main() then calls the function() using the jal instruction, which prints out the second string. Once the function() returns using the jr instruction, the main() program prints out the first string again.

Assemble the program, and slowly single-step the program. Watch the first string get printed out with $a0 pointing at the first string. When the jal instruction is performed, notice the program jump to the function(), and also notice that $ra is set pointing at the instruction after the jal. Watch the second string bring printed. When the jr instruction is performed, see the program jump back to the main() program.

Question: why did the main() program print out the second string and not the first string again? After all, the only value that the main() program puts into $a0 is the address of string1.

The answer is that the function() overwrote the value in $a0 when it printed out the second string, so when we returned back to main(), what main() thinks is in the $a0 register is no longer there. The function() has tromped all over main()'s register value!

3 Functions: What We Need

Some of the following is abstracted from Appendix A of Patterson and Hennessy's book.

You can see that, if we are going to call and return from functions properly, we need to do some things other than jal & jr to get it to work. Here are the things we need for functions to work:

The function caller needs to be able to provide a set of arguments, in a specific order, to the function. The function needs to be able to see these as local variables.
The function needs to be able to create its own local variables which are different to those in the functions which called it.
The function caller and the function itself are going to need to agree on how to store away register values, so that each will have access to the CPU's registers without having to worry about losing values.
The function needs to be able to return a result to the function caller.
We also want recursion: the ability to write functions which call themselves an arbitrary number of times.

In the following discussion, the function being called is going to be known as the callee.

3.1 Registers for Arguments and Result

On a CPU, there are two places which we could use to send in arguments to a function, and get back the result: registers or main memory. With the MIPS CPU, the registers $a0 to $a3 are used to send in up to 4 arguments to a function: if the function needs more, then the caller and callee must be written to store and collect the remaining arguments in main memory. The registers $v0 and $v1 are used to return a single result to the caller: both are used in combination if the result is a doubleword.

3.2 Who Deals Which Registers?

Of course, there are only 32 registers on the MIPS CPU, and both the function caller and the function will need to use some of them. Somebody is going to need to do some work in order to save the function caller's existing values, so that the function itself has some registers to use.

Here is the register saving convention used by all software written for the MIPS:

Registers $a0 to $a3 are used for arguments, and registers $v0 and $v1 for the return value. Similarly, the caller may also be using the temporary registers $t0 to $t7. These are all caller-saved registers: if the caller expects to use one of these registers after a call, it must save its value before the call.
A callee must save the values in these registers ($s0 ... $s7, $fp, and $ra) before altering them since the caller expects to find these registers unchanged after the call. These are callee-saved registers.

3.3 The Stack

So, the function caller stashes some registers away before it makes the function call. Likewise, the function callee stashes some registers away when it gets called. On the way back out, both the callee and caller restore the register values, so that when the function is done the caller has its registers back the way they were (except for the result of the function).

This is all fine and good if we only call one function at a time: we can choose a fixed set of memory locations and store the register values into these locations, then fetch them back later. But what about functions that call functions, and functions that perform recursion an arbitrary number of times? One fixed set of locations is not going to be enough.

This issue is solved using a stack. A stack is an area of memory of (essentially) arbitrary size which we can use to store as many register values as we like, as well as other data. We can push values onto the stack, which grows in size, and later we can pop values back off the stack in reverse order.

Stack (from Wikipedia)

Conventionally, memory on many computers is laid out so that the code of a program is stored in low memory, followed by any global data which has been allocated to the program. The stack is created at the high-end of memory and as it grows, it grows downwards in memory locations. In other words, computer stacks are upside down: a push makes it grow at the bottom, not the top!

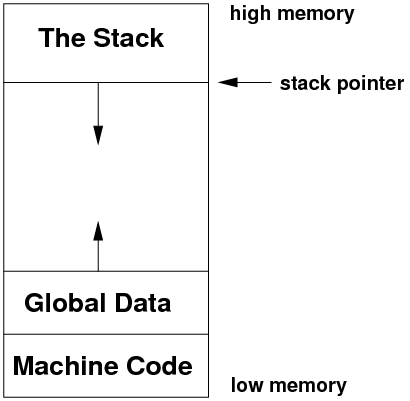This division of a program's memory into three distinct areas is not the only way to do things, but it does allow both the global data and the stack (where local data is stored) to expand with minimum risk of running into each other. Later, we will see how we can efficiently manage the memory allocated to all three.

Note the existence of the stack pointer, which points at the item most recently pushed onto the stack, and the item which is the first to be pulled. The MIPS register $sp is used as the stack pointer. The memory at addresses below the stack pointer is not yet allocated, but will become used once new data items are pushed onto the stack. When a program begins execution, the operating system will initialise the stack pointer to the highest address which is part of the stack.

3.4 Pushing and Popping

Pushing a data item onto the stack is easy: decrement $sp by the size of the item, and store the item on the stack using $sp indirect addressing. For example, to push the value in $t1 onto the stack:

        subu $sp, $sp, 4     # Decrement $sp by 4
        sw $t1, ($sp)        # and copy $t1 onto the stack

Popping a data item is the reverse. Let's pop the top word off the stack and bring it back into the $t3 register:

        lw $t3, ($sp)
        addu $sp, $sp, 4

Note: memory addresses start at 0 and go higher: there are no negative addresses. This explains why the addu and subu instructions are used.

3.5 Stack Frames

Even though I have shown you how to push and pop individual data items, in fact we will be growing and shrinking the stack in whole groups of data items. We know that each function has to keep track of:

the arguments passed to it from its caller
the address to return to when the function returns
any callee-saved registers that it saved when the function started up
any local variables which are accessible only to this function
when calling another function:
- any caller-saved registers that it must save before making the call
- any arguments to the function that it is calling

To do this, each function builds a stack frame on the stack which records all of these details. The stack frame has a generic format, although each frame's size will vary depending on how many arguments, saved registers and local variables are stored on it.

The simplest and smallest stack frame is shown in the diagram below; it is 24 bytes in size.

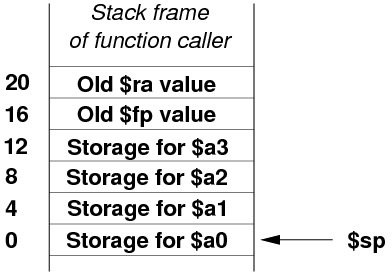The first thing we (as a function) must do when it is called is to move the stack pointer $sp down to make room on the stack for the frame. The next critical thing we need to do, then, is to save the return address currently in $ra. Why? Because if we ourselves now call another function, the return address that we need will be lost!

At the top of each function, therefore, should be these instructions or similar:

    function:  subu $sp, $sp, 24      # Make a stack frame of 24 bytes
               sw $ra, 20($sp)        # Save our $ra before we call another function
                                      # Note: we treat the stack frame like an array

And the last instructions in a function should undo the above two instructions:

               lw $ra, 20(sp)         # Reload our return address
               addu $sp, $sp, 24      # Destroy our stack frame
               jr $ra                 # and return out of this function

3.6 What About the Rest of the Stack Frame?

Good question! The minimal stack frame provides room for us, the recently-called function, to stash away copies of our arguments in $a0 to $a3, before we ourselves call a function. However, saving these registers is not mandatory: we only need to do it if we are calling another function.

Similarly, there is room to save our $fp register before we call a function which might destroy it.

Big note: in this subject we won't be using the $fp register at all, so there is no need for any function to save a copy of it on the stack frame.

Now, the stack frame shown above is simply the minimal, smallest stack frame. If we need to save other registers on the stack, then we will create a larger stack frame, and we get to choose where to put the extra values on the stack frame.

I've tried to find a definitive guide for what an extended MIPS stack frame should look like, but there does not seem to be any general agreement. So I recommend the following stack frame structure for this subject:

Obviously, you need to design your stack frame to hold those values that will get overwritten, but you don't need to make the stack frame any bigger than that.

3.7 Task 2

Download the program wk4stackframe1.asm and load it into MARS. This program does the same job as Task 1, but this time both the main() program and the function() create stack frames for themselves. This allows main() to keep the value in $a0 across the call to the function().

Run, and single-step, the program and make sure that you understand how the stack frame is working.

4 Local Variables

Functions also want to keep variables which are local, i.e. not globally visible and only within the scope of the function while it is running. If we used .data to store these variables, then the assembler would allocate space for them in the global data area, and everybody would be able to see them.

Instead, we can use the stack frame to store local variables. We need to:

increase the size of the stack frame to provide enough space to hold the local variables
decide where in this extended stack frame to place our local variables.

4.1 Task 3

Download the program wk4mostfreqchar.asm and load it into MARS. This program stores an array of characters on the stack frame as a local variable. In the C language, we would write this as the function definition:

    char mostfreqchar(void)
    {
      char line[200];    # Local array of 200 characters
       . . .
    }

In MIPS assembly, we need to allocate 200 more bytes on the stack frame, i.e. make it 224 bytes in length. We also need to decide where to store the line array. The simplest choice is to store it at offset 24 in the frame (i.e. just above the old $ra value), and extending for 200 bytes in length.

Read through the program and do these things:

Understand the purpose of the function, what inputs it receives (none), what result it returns.
Understand the high-level algorithm of the function. Note that it's often easier to use pointers into the array's contents rather than thinking in the array[index] mindset.
See how the stack frame is larger than the minimal stack frame, and that we take a pointer to the base of the character array, by doing 24($sp). That's because the local variable is at a fixed offset from the base of the stack frame.
Follow the assembly translation of the high-level algorithm. Writing this wasn't easy, mainly because you have to remember which register holds which variable. It's a good idea to scratch down on paper a table of register/variable equivalence.
Note that I chose to use registers which are caller-saved registers, so that I didn't have to save any registers in the function except for the $ra. This includes the argument registers $a0 to $a3: they were free as I didn't get any arguments.
Finally note that there is a fair bit of move $reg, $reg going on. That usually indicates that the allocation of registers could be improved, which would save having to copy values around here and there.

5 Recursion

We can now finally tackle recursion. For recursion to work, a function has to be able to call itself, and it also has to be able to keep its own local variables which will not be clobbered by other instances of the function.

For the local variables, we have to caller-save registers, callee-save registers, store locals in the stack frame, and/or all of the above.

Consider the prototypical recursive function, fact(X):

    int fact(int X) {
      int result;

      if (X==1) return(1);
      result= X * fact(X-1);
      return(X);
    }

Here, the X variable is both an argument to the function and a local variable in the function. Similarly, result is a local variable in the function. We don't have to worry too much about the value in result, as it is unknown before the recursive function call, and filled in by the recursive function call. However, the value in X has to be preserved across the function call, so we can multiply the result by X after the function call.

5.1 Task 4

Download the program wk4factorial.asm and load it into MARS. This program implements the recursive factorial function in MIPS assembly. Our argument (shown as X above) comes in as the $a0 register. Therefore, we need to preserve $a0 across the recursive call to the function. This is done by the sw $a0, 0($sp) instruction before the jal function call, and the lw $a0, 0,($sp) instruction after the return from the function.

5.2 Task 5

Using the wk4factorial.asm program as a template, write a MIPS assembly version of the recursive Fibonacci function. The definition of the function is:

Fib(1) = 1
Fib(2) = 1
Fib(X) = Fib(X-1) + Fib(X-2)

6 Outlook for the Next Lab

In the next lab, we will look at exceptions, interrupts and exception handling on the MIPS CPU.

File translated from T_EX by T_TH, version 3.85.
On 25 Nov 2011, 11:15.